Essence of Linear Algebra 1
3Blue1Brown 채널의 Essence of linear algebra 시리즈 정리한 내용입니다.
영상 : https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
vector(벡터) 는 세가지 학문의 측면에서 볼 수 있다.
- Physics : arrow in space. 길이와 방향을 가진다. 길이와 방향이 같으면 같은 벡터이다.
- Computer Science : list of numbers. 이때 숫자의 순서는 중요하다.
- Math : anything can be a vector. 더하고 곱하는 개념만 있으면 okay.
이 글에서는 "vector" 하면 xy좌표에 꼬리가 원점에 있는 화살표를 떠올리면 좋을 것 같다. 벡터의 좌표는 숫자쌍으로 되어있다.(Physics에서는 어디든지 자유롭다)

백터의 합은 다음 그림과 같이 움직임이 더해진 것이라고 생각하면 된다.

벡터의 곱하는 것도 마찬가지로, 벡터의 길이가 늘어지거나 줄어드는 것, 방향이 바뀌는 것이다. 이것을 scaling이라 하고, 변하는 정도를 scalar 이라 한다.

벡터를 묘사하는 숫자쌍을 하나의 scalar로 보자. 각 숫자는 벡터를 어떻게 늘이고 줄이는지에 대한 정보이다.
2차원 : $ \begin{bmatrix} x \\ y \\ \end{bmatrix} $
3차원 : $ \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} $
$\hat{i}$과 $\hat{j}$은 basis vector(기저벡터) of xy coordinate system 이다.
- $\hat{i}$ : x축의 unit vector(단위벡터). 오른쪽 방향의 길이 1 백터
- $\hat{j}$ : Y축의 unit vector(단위벡터). 위쪽 방향의 길이 1 백터

예를들어, $\begin{bmatrix} 3,-2 \end{bmatrix}$ 는 $(3)\hat{i} +(-2)\hat{j}$ 로 나타낼 수 있다.
Linear combination of $\vec{v}$ and $\vec{w}$ : $a\vec{v} + b\vec{w}$ (a와 b는 scalars)
Span of $\vec{v}$ and $\vec{w}$ : 주어진 벡터 합의 조합으로 나타넬수 있는 결과 벡터의 집합. (set of all their linear combinations, a와 b는 overall real numbers) 기본연산 가지고 도달 가능한 벡터의 집합.
2차원 벡터쌍의 span은 대부분 2차원 공간 전체가 되겠지만, 특정 선으로 제한되는 경우도 있다. 이 경우가 바로 linearly dependent 한 경우이다.
linearly dependent : span 축소없이 하나이상의 벡터를 제외시켜도 되는 경우.
3차원에서는 세번째 벡터가 두 벡터의 span위에 있거나 두 벡터의 span이 이미 선인 경우 등이 될 수 있다.
Linear combination of $\vec{v}$, $\vec{w}$, and $\vec{u}$ : $a\vec{v} + b\vec{w} + c\vec{u}$
$\vec{v}$ and $\vec{w}$ are linearly dependent : $\vec{u} = a\vec{v} + b\vec{w}$
반대로, 각 벡터가 기존 span에 다른 차원을 추가해주는 것이 가능하면 linearly independent 이라 한다.
linearly independent : $\vec{w} \neq a\vec{v}$ (for all values of a)
가장 중요한 Linear Transform에 대해 배워보자.
Transform은 function이다.
Linear은 두가지 속성을 의미한다.
1. lines remain lines
2. 원점은 변환 후에도 원점에 있어야 한다.
따라서, linear trnsform은 공간을 이동시키는 방법이다. 변형 이후에도 원점은 고정되어있어야하며, grid lines은 평행(parallel)하고 동일한 간격(evenly spaced)이여야 한다. 어렵게 생각하지 말자. 누누이 이야기 했듯이, $\hat{i}$ 과 $\hat{j}$ 이 어떻게 움직이는지만 알면 된다.
2x2 matrix $\begin{bmatrix} a & b\\ c&d \\ \end{bmatrix}$ 에서, a와 c는 $\hat{i}$ land 이고,b와 d는 $\hat{j}$ land이다.
이게 무슨소리인고 하니, 왼쪽 줄은 x가 움직이는것을, 오른쪽 줄은 y가 움직이는 방법을 알려준다. 각 축에 맞는 unit vector를 곱해주면 된다. 쉽죠?
$\begin{bmatrix} a & b\\ c&d \\ \end{bmatrix}$ $\begin{bmatrix} x \\ y \\ \end{bmatrix} = x \begin{bmatrix} a \\ c \\ \end{bmatrix} + y\begin{bmatrix} b \\ d \\ \end{bmatrix} = \begin{bmatrix} ax+by\\ cx+dy \\ \end{bmatrix} $
$\hat{i}$과 $\hat{j}$ 벡터가 linearly dependent 이라면, linear transform은 2차원 공간(space)를 squish시켜 두 벡터가 놓여있는 line으로 만든다.
linear transform을 여러번 적용 하는 것을 composition이라고 한다. 복잡하게 생각할 필요 없이, $\hat{i}$ 과 $\hat{j}$ 이 어떻게 움직이는지만 생각하자.
먼저 vector에 rotation 행렬을 곱한다. 그 후 shear행렬을 곱한다. 이것은 composition 행렬과 같다.

이것을 행렬간 곱(product) 으로 볼 수도 있다. 항상 행렬에서는 오른쪽 방향에서 왼쪽으로 봐야 한다.
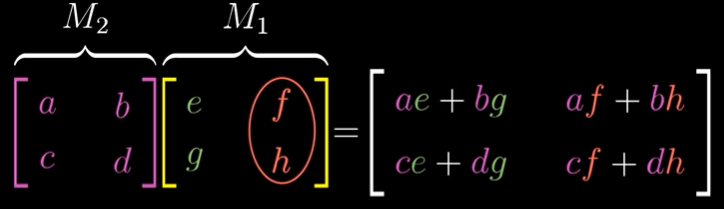
여기서 order does matter 라는 것을 기억하자. $AB \neq BA $ (항상 왼쪽에서 부터 적용하기 때문에 A(BC) = (AB)C 는 성립한다. 적용순서는 CBA다)
이제 determinant에 대해 알아보자.
determinant of transformation : 공간(area)이 바뀌는 정도를 나타내는 scaling factor
아래 그림에서, 1x1 =1 크기의 정사각형이 변환 후 6 크기의 직사각형이 되었다. 이 변환 정도가 determinant 이다. $det \begin{pmatrix} \begin{bmatrix} 3&0\\0&2 \end{bmatrix} \end{pmatrix} = 6$ 으로 나타낸다.

determinant 가 0이 되면 space가 squish 된다. 이때 행렬은 columns must be linearly dependent 이여야 한다.
determinant 가 방향이 바뀌면 음수가 된다.
식으로는 다음과 같이 표현할 수 있다.
$det \begin{pmatrix} \begin{bmatrix} a&b\\c&d \end{bmatrix} \end{pmatrix} = ad-bc$
ad는 변환 후 공간 넓이를 나타내며, bc는 둘다 0이 아닐 경우 공간이 얼마나 대각선 방향으로 늘려지거나 찌그려지는가를 나타낸다.

3차원은 다음과 같다.

$A\vec{x} = \vec{v}$ 일 때, (A는 transformation)
1. $det(A) \neq 0$ (공간 0으로 축소 안하는 경우)
특정 백터 $\vec{v}$ 로 변할 수 있는 백터는 항상 하나만 있다. 그리하여 하나의 해가 존재하고, 변환을 역으로 돌리면 $\vec{x}$를 찾을 수 있다. 역으로 변환하는 것을 inverse matrix(역행렬)이라 한다. A의 역행렬은 $A^{-1}$ 으로 표기한다.
$ A^{-1}A $은 아무것도 하지 않는 변환과 같으며, 이것을 identity transformation이라 한다. 따라서 다음과 같이 해를 찾을 수 있다.
$\vec{x} = A^{-1}\vec{v}$
2. $det(A) = 0$
$A^{-1}$ 존재하지 않는다. $\vec{v}$가 선 위에 놓여져 있는 경우에만 해를 구할 수 있다.